Graph: Depth-First Search and Breadth-First Search
定义
- 在图论中,由一个有向无环图组成的序列,只要满足下面两种情况则称为拓扑排序:
- 每个顶点只允许访问一次;若顶点A在图中存在到达顶点B的路径,则不会存在顶点B到顶点A的路径,也就是说这条路径是单向的;
问题
- 拓扑排序可用来解决什么问题呢?比如说课程排序,编译依赖,类似凡是涉及到相关顺序的时间安排;还可以用来判断一幅有向图是否无环。
两种排序方法
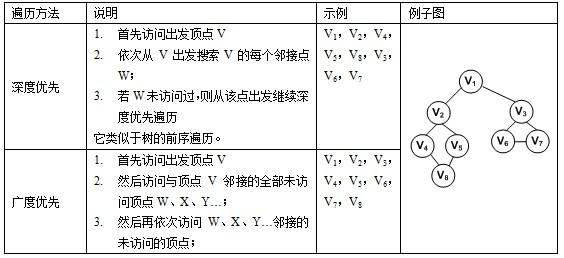
Breadth-First Search(BFS, 广度优先搜索)
方法
- 从有向图中选择一个没有前驱(即入度为0)的顶点并且输出它.
- 从网中删去该顶点,并且删去从该顶点发出的全部有向边.
- 重复上述两步,直到剩余的网中不再存在没有前趋的顶点为止.
实现
// C++ code
#include <iostream>
#include <vector>
#include <list>
#include <queue>
class Graph{
private:
int num_vertex;
std::vector< std::list<int> > AdjList;
int *color, // 0:白色, 1:灰色, 2:黑色
*distance, // 0:起點, 無限大:從起點走不到的vertex
*predecessor; // -1:沒有predecessor, 表示為起點vertex
public:
Graph():num_vertex(0){}; // default constructor
Graph(int N):num_vertex(N){ // constructor with input: number of vertex
// initialize Adjacency List
AdjList.resize(num_vertex);
};
void AddEdgeList(int from, int to);
void BFS(int Start);
};
void Graph::AddEdgeList(int from, int to){
AdjList[from].push_back(to);
}
void Graph::BFS(int Start){
color = new int[num_vertex];
predecessor = new int[num_vertex];
distance = new int[num_vertex];
for (int i = 0; i < num_vertex; i++) { // 初始化,如圖二(b)
color[i] = 0; // 0:白色;
predecessor[i] = -1; // -1表示沒有predecessor
distance[i] = num_vertex+1; // num_vertex個vertex,
} // 最長距離 distance = num_vertex -1條edge
std::queue<int> q;
int i = Start;
for (int j = 0; j < num_vertex; j++) { // j從0數到num_vertex-1, 因此j會走過graph中所有vertex
if (color[i] == 0) { // 第一次i會是起點vertex, 如圖二(c)
color[i] = 1; // 1:灰色
distance[i] = 0; // 每一個connected component的起點之距離設成0
predecessor[i] = -1; // 每一個connected component的起點沒有predecessor
q.push(i);
while (!q.empty()) {
int u = q.front(); // u 為新的搜尋起點
for (std::list<int>::iterator itr = AdjList[u].begin(); // for loop 太長
itr != AdjList[u].end(); itr++) { // 分成兩段
if (color[*itr] == 0) { // 若被「找到」的vertex是白色
color[*itr] = 1; // 塗成灰色, 表示已經被「找到」
distance[*itr] = distance[u] + 1; // 距離是predecessor之距離加一
predecessor[*itr] = u; // 更新被「找到」的vertex的predecessor
q.push(*itr); // 把vertex推進queue
}
}
q.pop(); // 把u移出queue
color[u] = 2; // 並且把u塗成黑色
}
}
// 若一次回圈沒有把所有vertex走過, 表示graph有多個connected component
// 就把i另成j, 繼續檢查graph中的其他vertex是否仍是白色, 若是, 重複while loop
i = j;
}
}
int main(){
Graph g1(9);
// 建立出圖二(a)的Adjacency List
g1.AddEdgeList(0, 1);g1.AddEdgeList(0, 2);g1.AddEdgeList(0, 3);
g1.AddEdgeList(1, 0);g1.AddEdgeList(1, 4);
g1.AddEdgeList(2, 0);g1.AddEdgeList(2, 4);g1.AddEdgeList(2, 5);g1.AddEdgeList(2, 6);g1.AddEdgeList(2, 7);
g1.AddEdgeList(3, 0);g1.AddEdgeList(3, 7);
g1.AddEdgeList(4, 1);g1.AddEdgeList(4, 2);g1.AddEdgeList(4, 5);
g1.AddEdgeList(5, 2);g1.AddEdgeList(5, 4);g1.AddEdgeList(5, 8);
g1.AddEdgeList(6, 2);g1.AddEdgeList(6, 7);g1.AddEdgeList(6, 8);
g1.AddEdgeList(7, 2);g1.AddEdgeList(7, 3);g1.AddEdgeList(7, 6);
g1.AddEdgeList(8, 5);g1.AddEdgeList(8, 6);
g1.BFS(0);
return 0;
}
template<int max_size>
void Graph<max_size>::BFS(List<Vertex>& output) const
{
output.clear();
int in_degree[max_size];
//入度置零
for (int i = 0; i < max_size; i++)
in_degree[i] = 0;
//1)计算初始入度:
for (Vertex v = 0; v < count; v++) {
Vertex w;
for (int i = 0; i < neighbours[v].size(); i++) {
neighbours[v].retrieve(i, w);
in_degree[w]++;
}
}
queue<Vertex> wait;
for (Vertex v = 0; v < count; v++) //2)第一轮度数为0的点入队
if (in_degree[v] == 0)wait.push(v);
while (!wait.empty()) {
Vertex x = wait.front();
output.insert(output.size(), x); //3)取出队首放入output
Vertex w;
for (int i = 0; i < neighbours[x].size(); i++) {//4)“邻居”节点入度--
neighbours[x].retrieve(i, w);
in_degree[w]--;
if (in_degree[w] == 0)wait.push(w);
}
wait.pop();
}
}
Depth-First Search(DFS,深度优先搜索)

实现
// C++ code
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <iomanip> // for std::setw()
class Graph{
private:
int num_vertex;
std::vector< std::list<int> > AdjList;
int *color, // 0:white, 1:gray, 2:black
*predecessor,
*discover,
*finish;
public:
Graph():num_vertex(0){};
Graph(int N):num_vertex(N){
// initialize Adj List
AdjList.resize(num_vertex);
};
void AddEdgeList(int from, int to);
void BFS(int Start); // 定義見上一篇文章
void DFS(int Start);
void DFSVisit(int vertex, int &time);
};
void Graph::DFS(int Start){
color = new int[num_vertex]; // 配置記憶體位置
discover = new int[num_vertex];
finish = new int[num_vertex];
predecessor = new int[num_vertex];
int time = 0; // 初始化, 如圖三(b)
for (int i = 0; i < num_vertex; i++) {
color[i] = 0;
discover[i] = 0;
finish[i] = 0;
predecessor[i] = -1;
}
int i = Start;
for (int j = 0; j < num_vertex; j++) { // 檢查所有Graph中的vertex都要被搜尋到
if (color[i] == 0) { // 若vertex不是白色, 則進行以該vertex作為起點之搜尋
DFSVisit(i, time);
}
i = j; // j會把AdjList完整走過一遍, 確保所有vertex都被搜尋過
}
}
void Graph::DFSVisit(int vertex, int &time){ // 一旦有vertex被發現而且是白色, 便進入DFSVisit()
color[vertex] = 1; // 把vertex塗成灰色
discover[vertex] = ++time; // 更新vertex的discover時間
for (std::list<int>::iterator itr = AdjList[vertex].begin(); // for loop參數太長
itr != AdjList[vertex].end(); itr++) { // 分成兩段
if (color[*itr] == 0) { // 若搜尋到白色的vertex
predecessor[*itr] = vertex; // 更新其predecessor
DFSVisit(*itr, time); // 立刻以其作為新的搜尋起點, 進入新的DFSVisit()
}
}
color[vertex] = 2; // 當vertex已經搜尋過所有與之相連的vertex後, 將其塗黑
finish[vertex] = ++time; // 並更新finish時間
}
int main(){
// 定義一個具有八個vertex的Graph
Graph g2(8);
// 建立如圖三之Graph
g2.AddEdgeList(0, 1);g2.AddEdgeList(0, 2);
g2.AddEdgeList(1, 3);
g2.AddEdgeList(2, 1);g2.AddEdgeList(2, 5);
g2.AddEdgeList(3, 4);g2.AddEdgeList(3, 5);
// AdjList[4] is empty
g2.AddEdgeList(5, 1);
g2.AddEdgeList(6, 4);g2.AddEdgeList(6, 7);
g2.AddEdgeList(7, 6);
g2.DFS(0); // 以vertex(0), 也就是vertex(A作為DFS()的起點
return 0;
}
Reference
- 初學者寫給初學者的演算法教學
- https://www.jianshu.com/p/70952b51f0c8